Rechenregeln der Addition
Distributivgesetz der Multiplikation, Eigenschaften der Einheitsmatrix
Existenz der Inversen, Nchtkommutativität der Multiplikation, daher Multiplikation von links
Der Leistungskurs Mathematik schreibt zur Zeit die Facharbeit, so dass sich der vorangegangene Unterricht häufig mit der Vorbereitung der Arbeit und der Einführung in Themenfelder, deren Vertiefung spätere Themen der Facharbeit wurden, beschäftigte. Dies führte und führt zum Teil zu organisatorischen Schwierigkeiten des Unterrichtsganges. Der Fachlehre und ich lösten diese Schwierigkeiten dadurch, dass wir uns Themen aufteilten und sich der Fachlehrer verstärkt um die Facharbeit kümmern konnte und kann, währenddessen ich den Unterricht seit ca. vier Wochen fortführe. Diese Situation führt oft zu einem Lehrerwechsel während einer Doppelstunde, der die Lerngruppe m. E. jedoch nicht verunsichert, da wir themenfremd unterrichten.
Der Leistungskurs Mathematik des 12. Jahrgangs setzt sich aus elf Schülerinnen und drei Schülern zusammen. Auffällig ist die mündliche Beteiligung des Kurses im Unterricht. C., S., B. und B. beteiligen sich sehr oft mündlich und sind in der Lage, den Unterricht voranzubringen. N., S., M., K., K., H. und M. beteiligen sich zögerlicher, aber auch mit guten Beiträgen. N. und M. fallen dabei zudem auch durch sehr gute Beiträge auf. Die übrigen Schülerinnen und Schüler halten sich in der mündlichen Beteiligung stark zurück, obwohl sie in der Lage sind, sich auf fachlicher Ebene zu äußern und somit auch den Unterricht voranbringen könnten. N. erzielt schriftlich gute bis sehr gute Leistungen, bringt sich allerdings bislang selten in den Unterricht ein. Seine Beteiligung wird manchmal stärker, wenn es sich um Beweise mathematischer Inhalte handelt. F. und S. beteiligen sich sehr selten und überwiegend reproduktiv.
Erhalten die Schülerinnen und Schüler einen Arbeitsauftrag, den sie in Einzel- oder Partnerarbeit bearbeiten sollen, arbeiten alle konzentriert. Bei der Vorstellung der Ergebnisse steigert sich im Allgemeinen die mündliche Beteiligung, so dass ich diese Sozialform einsetze, um auch den schwächeren Schülerinnen und Schülern die Gelegenheit zu geben, sich in den Unterricht einzubringen.
Dieses Verhalten ist mir auch bei Hospitationen in einem Geschichtsgrundkurs des 12. Jahrgangs aufgefallen. Die mündliche Beteiligung des gesamten Kurses ist sehr schwach, wobei sich in Arbeitsphasen alle Schülerinnen und Schüler konzentriert mit den Aufgaben beschäftigen. In diesem Kurs befinden sich einige Schülerinnen und Schüler des Mathematikleistungskurses, die auch hier das gleiche Beteiligungsverhalten zeigen, sich aber selbst in den Phasen der Vorstellung der Ergebnisse stark zurückhalten.
Die Lerngruppe ist in der Lage, selbständig mit mathematischen Problemen umzugehen und eine Lösungsstrategie zu entwickeln. Sie können miteinander arbeiten und gehen aufeinander ein. In diesem Leistungskurs wird ein Computeralgebrasystem, der TI-92, eingesetzt, welches die meisten Schülerinnen und Schüler mittlerweile gut bedienen können.
Nach obenDie vorliegende Stunde vereint die Ergebnisse der bisherigen Unterrichtseinheit und soll den Schülerinnen und Schülern verdeutlichen, dass die Matrizenrechnung außerhalb der Schule einen hohen Stellenwert einnimmt. Im vorangegangenen Unterricht wurden die Themen Addition, Multiplikation von Matrizen, Lösen von Linearen Gleichungssystemen, Existenz und Bestimmung von der Inversen einer Matrix behandelt. Diese bislang behandelten Inhalte sollen nun miteinander verknüpft und auf ein Problem der Wirtschaftsmathematik übertragen werden. In der folgenden Stunde sollen mathematische Inhalte vertieft werden.[1]
In der vorangegangenen Stunde wurde die Erstellung eines Linearen Gleichungssystems am Beispiel eines stark vereinfachten Stücklistenproblems behandelt und per Hand gelöst, so dass in der vorliegenden Stunde auf die Kenntnis des Erstellens eines Linearen Gleichungssystems zurückgegriffen werden kann.[2]
Der TI-92[3] wurde in der Unterrichtseinheit als Hilfsmittel eingesetzt, nachdem die Grundlagen der jeweiligen Themen den Schülerinnen und Schülern vermittelt waren.
Nach obenStücklistenprobleme treten in der Wirtschaft auf. Dabei geht es um die Verflechtung von Produktionsschritten und deren Zwischen- und Endprodukten. Produziert eine Firma ein Produkt, so setzt sich dieses zumeist aus mehreren verschiedenen Einzelprodukten zusammen, die wiederum aus unterschiedlichen Komponenten bestehen können. Bei der Fertigung dieser Produkte muss die Anzahl der einzelnen Komponenten bzw. Zwischenprodukte bekannt sein, um einen reibungslosen Betrieb sicherzustellen. Wenn nicht nur das Endprodukt, sondern auch die Zwischenprodukte verkauft werden, wie es z. B. in der Automobilindustrie üblich ist[4], erhöhen sich die Stückzahlen der Einzelprodukte nicht nur um die geforderte Nachfrage, sondern auch um den Bedarf, der benötigt wird, um die Einzelprodukte herzustellen.
Es geht daher um die Frage, wie groß die Anzahl der verschiedenen Zwischen- und Endprodukte jeweils sein muss, um die Anfrage von außen decken zu können. Diese Frage kann mit Linearen Gleichungssystemen beantwortet werden. In der Praxis jedoch bedient man sich der Matrizenrechnung aufgrund der Vielzahl von Zwischen- und Endprodukten.
Zu Beginn der Überlegungen steht die graphische Darstellung der Verflechtung der einzelnen Produkte untereinander, ein sogenannter "Gozintograph"[5], der anschaulich beschreibt, welche Produkte und welche Anzahl (Mengeneinheiten) der jeweiligen Produkte für die Fertigung der übergeordneten Produkte nötig sind. Daraus ergibt sich die Erstellung einer Verflechtungstabelle in technologischer Reihenfolge[6] z. B.
für |
x1 | x2 | x3 | x4 | x5 | x6 |
| x1: Draht | 0 | 20 | 0 | 6 | 8 | 10 |
| x2: Spule | 0 | 0 | 0 | 1 | 3 | 2 |
| x3: Widerstand | 0 | 0 | 0 | 2 | 1 | 1 |
| x4: Bauteil A | 0 | 0 | 0 | 0 | 0 | 2 |
| x5: Bauteil B | 0 | 0 | 0 | 0 | 0 | 1 |
| x6: Apparat | 0 | 0 | 0 | 0 | 0 | 0 |
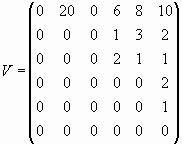. Diese Matrix wird auch als Input-Output-Matrix[8] bezeichnet. Betrachtet man nun den internen Bedarf der Produktion und die externe Bestellung 
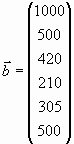, so ergibt sich für den Produktionsvektor 
(Anzahl der herzustellenden Produkte), dass 
(1) ist. Diese Gleichung lässt sich zu der Form 
(2) umformen, so dass nach der Eingabe der Daten in einen Computer sofort der Produktionsvektor ausgegeben wird. Bei der Umformung müssen die Rechenregeln für Matrizen beachtet und die Existenz der Inversen 
begründet werden, die sich aus der besonderen Dreiecksgestalt der Matrix V und der Differenz 
ergibt[9], z. B.:
Rechenregeln der Addition
Distributivgesetz der Multiplikation, Eigenschaften der Einheitsmatrix
Existenz der Inversen, Nchtkommutativität der Multiplikation, daher Multiplikation von links
Daraus lässt sich für Stücklistenprobleme solcher Form eine allgemeine Regel formulieren:
Produktionsvektor = (Einheitsmatrix – Verflechtungsmatrix)-1 . Bestellvektor
Es ergibt sich in dem zu behandelnden Beispiel:
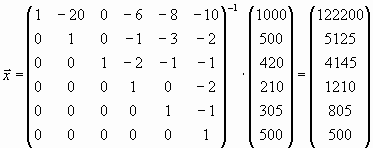Durch die Aufstellung eines Linearen Gleichungssystems vorab ist es möglich, die Gleichung (1) oder durch eine Umformung des Systems die Gleichung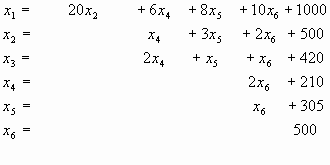 
(3) zu erhalten, z. B. für (1):
In dem Beispiel ist das Lineare Gleichungssystem noch einfach zu finden und zu lösen, in der Praxis handelt es sich allerdings um wesentlich größere Listen ("z. B.: BASF/Chemie: Matrizen mit etwa 10000 Zeilen"[10]), so dass ein Gleichungssystem nicht mehr praktikabel ist und die Verflechtungsmatrix zur Anwendung kommt.
Vertiefend kann nachfolgend in einer weiteren Stunde die Inverse näher betrachtet und auf den Zusammenhang: 
eingegangen werden.[11]
Die Behandlung der Matrizen im Leistungskurs wird von den Rahmenrichtlinien als Erweiterungsthema genannt.[12] Mit Hilfe der Matrizenrechnung lassen sich auf einfache Weise Lineare Gleichungssysteme lösen, wenn ein geeignetes Hilfsmittel, wie der TI-92, der an dem Käthe-Kollwitz-Gymnasium im Leistungskurs eingeführt ist, mit einem installierten Computeralgebrasystem, zur Verfügung steht. Ebenso können algebraische Strukturen auf die Matrizen übertragen werden. Die Behandlung von Matrizen im Unterricht wird zudem noch durch die Durchführung der Facharbeit sinnvoll, da sich in Verbindung mit der Matrizenrechnung Themen für die Facharbeit ergeben.
Anwendungsorientierung ist ein häufig gefordertes Teilgebiet im Mathematikunterricht.[13] Die Rahmenrichtlinien verweisen direkt darauf, den "Anwendungsbezug zu beachten"[14]. Durch neue technische Möglichkeiten - Computeralgebrasysteme, die auf einem tragbaren Rechner installiert sind, wie z. B. der TI-92 – werden rechenintensive Anwendungen für den Unterricht einsetzbar, da das Computeralgebrasystem "das oft mühsame kalkülmäßige Abarbeiten von Routineaufgaben"[15] für die Schülerinnen und Schüler übernehmen kann. Dies setzt jedoch voraus, dass die Schülerinnen und Schüler das Kalkül, z. B. die Lösung von Linearen Gleichungssystemen, beherrschen.
Ein Anwendungsbezug dient nach "Laugwitz [...] der außermathematischen Motivierung"[16] der Schülerinnen und Schüler. Auch wenn Anwendungsaufgaben häufig konstruiert und idealisiert sind[17], so können sie dennoch genutzt werden, "weil mit ihnen am ehesten gezeigt werden kann, daß [sic] und wie Mathematikunterricht alle betrifft."[18] So kann Schülerinnen und Schülern vermittelt werden, dass die mathematischen Inhalte auch außerhalb der Schule eine große Rolle spielen. Die Matrizenrechnung hat hierbei den Vorteil, "dass manchmal [reale] Zusammenhänge recht einfach mit Hilfe von Matrizen beschrieben werden können, während die praktische Berechnung dann einem Rechner überlassen werden kann."[19]
Hinzu kommt bei Anwendungsaufgaben die Anforderung des Mathematisierens: Die Übersetzung einer realen Situation in die Mathematik. Die mathematische Lösung tritt dabei manchmal in den Hintergrund, da die Lösungsverfahren bekannt sind. Größere Bedeutung gewinnt dann wieder die Interpretation des Ergebnisses.[20]
Das Stücklistenproblem ist ein Anwendungsbeispiel, das praktische Relevanz besitzt und, obwohl es für den Unterricht idealisiert wurde, doch in dieser Weise genutzt wird. Neben Stücklistenproblemen können Codierungs- oder Populationsprobleme als Anwendung der Matrizenrechnung behandelt werden. Populationsprobleme scheiden als Thema dieser Stunde aus, da ein Thema der Facharbeit sich mit diesem Problem beschäftigt. Ich habe ein Stücklistenproblem gewählt, weil es für die Schülerinnen und Schüler verständlich ist und alle zuvor behandelten Unterrichtsinhalte benötigt werden, um das Problem zu lösen. Die Aufgabe dieser Stunde ließe sich zwar noch per Hand lösen, doch geht es um eine Umsetzung für die Praxis, die mit Hilfe von Matrizen durchgeführt wird. Diese unterscheidet sich prinzipiell nicht von der Umsetzung der Schülerinnen und Schüler, was ich aufgrund des Realitätsbezuges als Vorteil sehe.
Die größte Schwierigkeit des Stücklistenproblems besteht in dem Verständnis des "internen Bedarfs" und der sich daraus ergebenden "Verflechtungsmatrix". Tietze, Klika und Wolpers geben den Schülerinnen und Schülern diesen Zusammenhang vor.[21] Ich möchte hingegen die didaktische Reduktion darin vornehmen, vorerst auf die Verflechtungsmatrix zu verzichten, diese wird sich aus dem Linearen Gleichungssystem ergeben.[22] Ebenso beschränke ich die Mathematisierung auf den Gozintographen, in dem der späteren Übersichtlichkeit wegen bereits Variablen den Produkten zugeordnet sind, um Zeit für die innermathematische Behandlung der Gleichungsumformung zu gewinnen. Aus diesem Grund wurde in der vorangegangenen Stunde auch die Erstellung eines Linearen Gleichungssystems an einer ähnlichen, jedoch stark vereinfachten Aufgabe vorgenommen. In einer erneuten Aufgabe kann die Mathematisierung durch die Erstellung eines Gozintographen geübt werden.[23]
Die Gleichungsumformung ist ein wichtiger Bestandteil der Stunde, weil dadurch der Produktionsvektor direkt berechnet werden kann und der Zusammenhang mit den bisherigen Unterrichtsinhalten deutlich wird. Die Schülerinnen und Schüler sollen sich hierbei der Inhalte erinnern und ihre Fähigkeit des Argumentierens und Begründens[24] schulen und sich in der Verwendung der Fachsprache üben. Allein die Eigenschaft, dass die Matrizenmultiplikation in der Regel nicht kommutativ ist, bereitet den Schülerinnen und Schülern häufig Schwierigkeiten, so dass auf eine Begründung ihres Vorgehens nicht verzichtet werden darf. Das Ergebnis der Umformung hingegen kann dann einen Beitrag zur Fähigkeit der Generalisierung und der Interpretation leisten, indem es in die "reale" Situation zurückübersetzt wird, um eine Formel zu gewinnen.
Die Gleichungsumformung vereint hierbei die in der Einheit behandelten Unterrichtsinhalte, dient demnach der Wiederholung und der Festigung. Die Lösung des Linearen Gleichungssystems jedoch ist für die Schülerinnen und Schüler Routine, so dass diese Tätigkeit von dem Computeralgebrasystem übernommen werden kann.[25]
Nach obenZu Beginn der Stunde werde ich den Schülerinnen und Schülern einführend das Stücklistenproblem mit Hilfe einer Folie, auf der die Aufgabe abgebildet ist, vorstellen. Die Schülerinnen und Schüler erhalten dann die Aufgabe als Kopie und sollen in Einzel- oder Partnerarbeit ein zur Lösung geeignetes Lineares Gleichungssystem aufstellen. Um Verunsicherungen bei der späteren Ergebnissicherung zu vermeiden, sind dabei bereits Variablen für die Einzelteile angegeben. Alternativ könnte diese Phase im Unterrichtsgespräch durchgeführt werden, doch eignet sich eine Einzel- oder Partnerarbeit m. E. in Hinblick auf die Lerngruppe besser.[26] In dieser Phase sollen die Schülerinnen und Schüler auf bereits Gelerntes zurückgreifen und dieses auf eine neue Situation übertragen.
Anschließend sollen sie ihre Ergebnisse vorstellen, welche von mir an der Tafel festgehalten werden, um sicherzustellen, dass die Schülerinnen und Schüler eine einheitliche Lösung des Arbeitsauftrags für den weiteren Verlauf der Stunde zur Verfügung haben. Das an der Tafel festgehaltene Lineare Gleichungssystem soll nun in Matrizen übertragen werden, um es im Fortgang der Stunde mit Hilfe des TI-92 zu lösen. Die Schülerinnen und Schüler sollen sich in einer kurzen Einzel- oder Partnerarbeit mit der Übertragung beschäftigen, um einen offeneren Zugang zu ermöglichen.[27]
Es sind zwei Möglichkeiten der Übertragung des Systems denkbar, je nachdem welche Gestalt das System besitzt.[28]
(1) zu bestimmen. Dabei sollen die Gesetze der Matrizenrechnung einfließen, die die Schülerinnen und Schüler als Begründung ihrer Umformung nennen sollen. Nach der Umformung sollen die Schülerinnen und Schüler nun mit Hilfe des TI-92 in Einzelarbeit den Produktionsvektor berechnen. An dieser Stelle besteht die Möglichkeit, den Unterricht zu beenden und die Berechnung als Hausaufgabe zu stellen.
(3)Die Schülerinnen und Schüler werden voraussichtlich nicht die Gleichung (3), sondern folgende Form erstellen: 
(4). Diese Gleichung läßt sich mit Hilfe des TI-92 mittels des Gaußschen Lösungsalgorithmus sofort lösen und die eigentliche Fragestellung hierdurch beantworten. Allerdings wird dabei nicht klar, welches Verfahren in der Praxis angewendet wird. Um aber die "reale" Verfahrensweise den Schülerinnen und Schülern zu vermitteln, werde ich ihnen bekannt geben, dass in der Praxis die Gleichung (1) angewendet wird. Die Schülerinnen und Schüler sollen dann im Unterrichtsgespräch einen Zusammenhang zwischen der Gleichung (4) und der Gleichung (1) herstellen.
ist. Die Schülerinnen und Schüler sollen nun die Matrix V berechnen und deren Bedeutung erkennen und formulieren. Möglich ist dabei auch, den Zusammenhang direkt aus dem aufgestellten Linearen Gleichungssystem zu erkennen. Aus der Beschäftigung ergeben sich dann die Begriffe "Verflechtungsmatrix", "interner Bedarf" und "externe Bestellung". Obwohl wie oben beschrieben die Gleichung (4) schnell zu lösen ist, werde ich anregen, eine Ausgabe für den Produktionsvektor zu erhalten, die sofort liefert, und nicht den Umweg über den Gaußschen Lösungsalgorithmus beschreitet. Hierbei müssen die Kenntnisse über die Inverse einer Matrix eingebracht werden.
Anschließend sollen die Schülerinnen und Schüler mit Hilfe des TI-92 und der umgeformten Gleichung die Lösung in Einzelarbeit berechnen. Diese Aufgabe könnte als Hausaufgabe dienen.
c) Die Schülerinnen und Schüler entwickeln während ihrer Einzel-/Partnerarbeitsphase beide Gleichungen. In diesem Fall sollen sie einen Zusammenhang zwischen den Gleichungen herstellen. Der weitere Unterrichtsverlauf richtet sich nach b).
Sollten die Schülerinnen und Schüler große Schwierigkeiten während der Umsetzung des Gleichungssystems in Matrizen oder bei der Erklärung der Bedeutung der jeweiligen Matrizen haben, so könnte der Unterricht beendet werden, wenn die Gleichung (1) (Fall a)) oder die Gleichungen (1) und (4) bzw. (3) (Fall b), c)) erarbeitet worden sind. Die Umformung mit den jeweiligen Begründungen oder die Erklärung der Bedeutung der Matrix und der Vektoren könnte dann als Hausaufgabe dienen.
Im Plenum soll nun die Bedeutung des Ergebnisses formuliert und eine Formel für solche Probleme angegeben und von mir an der Tafel festgehalten werden. (Geplantes Unterrichtsende)
Als didaktische Reserve besteht zudem die Möglichkeit, das Verfahren zu bewerten. Wann ist dieses Verfahren sinnvoll? Für wen oder welche Firmen ist dieses Verfahren sinnvoll? Hat es gegenüber der Aufstellung eines Linearen Gleichungssystems Vorteile?
oder auch 
gelangen. Bei solcher Vorgehensweise kämen auch experimentelle Elemente in die Arbeit der Schülerinnen und Schüler hinein. Dafür halte ich aber den Kurs für zu inhomogen. Einzelne Schülerinnen und Schüler könnten das Problem sicherlich lösen und auch die mathematischen Feinheiten erkennen, der Großteil jedoch würde die mathematischen Schwierigkeiten übersehen und sich nur auf den TI-92 verlassen. Daher denke ich, dass sie wissen müssen, welche innermathematischen Operationen sie durchführen müssen, um zu der Problemlösung zu kommen. Aus diesem Grund werden die innermathematischen Überlegungen im Unterrichtsgespräch angestellt. Als Hausaufgabe wird ein weiteres Stücklistenproblem gestellt, zu dem die Schülerinnen und Schüler auch den Gozintographen erstellen sollen.
Nach obenDie Schülerinnen und Schüler sollen
| Phase | Inhalte | Medien Sozialform |
|---|---|---|
| Einstieg | - Vorstellung des Problems durch den Lehrer anhand einer Folie mit der Aufgabe, Verteilen der Aufgabe. Wie viele Einzelteile und Apparate muss der Betrieb herstellen? | LV/Kopie/ Folie/OHP |
| Erarbeitung I | - Aufstellen eines Linearen Gleichungssystems (LGS) durch die Schülerinnen und Schüler. | Einzel- oder Partnerarbeit |
| Ergebnissicherung | - Vergleichen der Ergebnisse. - Notierung durch den Lehrer an der Tafel. |
L-S-GTafel |
| Erarbeitung II | - Übertragung des LGS in Matrizen.a) - Erläuterung der Bedeutung der Matrix und der Vektoren in der Praxis durch die Schülerinnen und Schüler.
Mögliches Stundenende (Hausaufgabe: Umformung).- Umformung der Gleichung mit Begründungen. |
Einzel- oder PartnerarbeitTafelL-S-G |
| b) und c) - Umformung der Gleichung mit BegründungenMögliches Stundenende (Hausaufgabe: Erläuterung der Bedeutung der Matrix und der Vektoren).- Erläuterung der Bedeutung der Matrix und der Vektoren in der Praxis durch die Schülerinnen und Schüler. | L-S-GTafel | |
| Mögliches Unterrichtsende | ||
| Ergebnissicherung | - Berechnung des Ergebnisses mit Hilfe des TI-92. - Formulierung einer Lösungsformel für Stücklistenprobleme. | EinzelarbeitL-S-GTafel |
| Geplantes Unterrichtsende | ||
| Reserve | - Beurteilung und Kritik des Lösungsverfahrens. | L-S-G |
| - Stellung der Hausaufgabe. | Kopie | |
Eine Elektronikfirma verkauft einen selbst hergestellten elektrischen Apparat und auch dessen Einzelteile.
Die folgende Grafik veranschaulicht, wie viele Einzelteile für die Produktion des Apparates benötigt werden und wie die Einzelteile miteinander kombiniert werden.
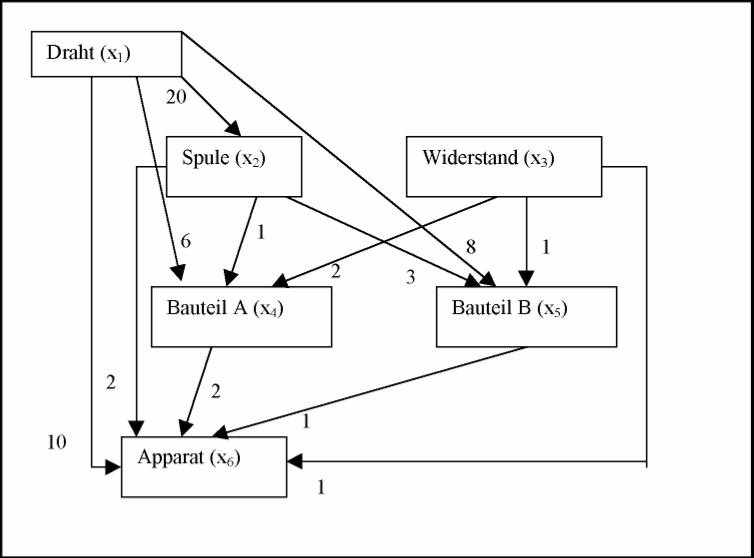
Ein Kunde bestellt 1000 Einheiten Draht, 500 Spulen, 420 Widerstände, 210 Bauteile A, 305 Bauteile B und 500 Apparate. Wie viele Einzelteile und Apparate muss die Firma produzieren, um die Bestellung erfüllen zu können.
Stellen Sie hierzu ein geeignetes Lineares Gleichungssystem auf!
2. Hausaufgabe
Zur Herstellung eines Mess- und Steuergerätes benötigt man integrierte Schaltungen und verschiedene Einzelteile. Ein solches Gerät wird aus 2 Platinen, einem Bauteil A und 3 Schaltungen der Form IV zusammengebaut. Das Bauteil A besteht aus einer Platine, 2 Schaltungen der Form III und 4 Schaltungen der Form IV. Für die Produktion einer Platine benötigt man 2 Schaltungen der Form I, 3 Schaltungen der Form II, eine Schaltung der Form III und 2 Schaltungen der Form IV.
An Bestellungen liegen vor: 10000 Schaltungen der Form I, 10000 Schaltungen der Form II, 10000 Schaltungen der Form III, 15000 Schaltungen der Form IV, 1000 Platinen, 300 Bauteile A und 500 Geräte.
Erstellen Sie eine Grafik und berechnen Sie die erforderliche Produktion der einzelnen Teile!
Nach oben
1 siehe Sachanalyse. Zurück
2 siehe Didaktische Überlegungen. Zurück
3 Ein mit einem Computeralgebrasystem ausgerüsteter "Taschenrechner". Zurück
4 vgl. Kroll, Wolfgang; Reiffert, Hans Peter; Vaupel, Jürgen: Analytische Geometrie/Lineare Algebra. Grund- und Leistungskurs. Bonn 1997, S. 162. Zurück
5 siehe Anhang. Zurück
6 z. B.: wird für benötigt, wiederum für, usw. Diese Reihenfolge ist nicht immer eindeutig. Zurück
7 In der Literatur findet sich auch die Bezeichnung der "Mengenmatrix", so bei: Schanz, Rainer; Schmidt, Günther (Hg.): Lineare Algebra. Materialien zum Grund- und Leistungskurs der Mainzer Studienstufe. Mainz 1981, S. 30-34. Kemeny, John G.; Schleifer jr., Arthur; Snell, J. Laurie; Thompson, Gerald L.: Mathematik für die Wirt-schaftspraxis. 2. verb. Aufl., Berlin und New York 1972, S. 272 f. Zurück
8 Ministerium für Bildung, Wissenschaft und Weiterbildung Rheinland-Pfalz (Hg.): Materialien zum Mathema-tikunterricht mit Computer und DERIVE. Landesmedienzentrum Koblenz 1995-1996, S. 5.32. Zurück
9 vgl. auch Griesel, Heinz; Postel, Helmut (Hg.): Mathematik heute. Leistungskurs Lineare Algebra/Analytische Geometrie, Lösungen und didaktisch-methodischer Kommentar. Hannover 1988, S. 94-97. Zurück
10 Schanz; Schmidt (Hg.): Lineare Algebra, S. 38. Zurück
11 vgl. Tysiak, Wolfgang: Multiplikation von Produktionsmatrizen und Gozinto-Verfahren. In: Der mathematische und naturwissenschaftliche Unterricht. Jahrgang 51, Heft 4, Bonn 1998, S. 212-217. Zurück
12 Niedersächsisches Kultusministerium (Hg.): Rahmenrichtlinien für das Gymnasium, gymnasiale Oberstufe. Ma-thematik. Hannover 1991, S. 13. Zurück
13 Förster, F.; Reichel, H. C.: Was ist "Anwendungsorientierter Mathematikunterricht"? In: Hischer, Horst & Weiß, Michael (Hg.): Fundamentale Ideen. Zur Zielorientierung eines künftigen Mathematikunterrichts unter der Berück-sichtigung der Informatik. Hildesheim 1995, S. 78. Zurück
14 Niedersächsisches Kultusministerium (Hg.): Rahmenrichtlinien für das Gymnasium, S. 17. Zurück
15 Förster; Reichel: Was ist "Anwendungsorientierter Mathematikunterricht"?, S. 82. Zurück
16 Tietze, Uwe-Peter; Klika, Manfred; Wolpers, Hans: Didaktik des Mathematikunterrichts in der Sekundarstufe II. Braunschweig/Wiesbaden 1982, S. 193. Zurück
17 siehe Sachanalyse. Zurück
18 Führer, Lutz: Pädagogik des Mathematikunterrichts. Eine Einführung in die Fachdidaktik für Sekundarstufen. Braunschweig/Wiesbaden 1997, S. 118. Zurück
19 Tysiak, W.: Multiplikation von Produktionsmatrizen, S. 217. Zurück
20 Humenberger, J. & Reichel, H.-Ch.: Fundamentale Ideen der Angewandten Mathematik und ihre Umsetzung im Unterricht. Mannheim; Leipzig; Wien; Zürich 1995, S. 64. Niedersächsisches Kultusministerium (Hg.): Rahmen-richtlinien für das Gymnasium, S. 7. Zurück
21 Tietze; Klika; Wolpers: Didaktik des Mathematikunterrichts. S. 169 f. Zurück
22 siehe Methodische Überlegungen. Zurück
23 siehe Anhang: Hausaufgabe. Zurück
24 Tietze; Klika; Wolpers: Didaktik des Mathematikunterrichts. S. 26. Zurück
25 vgl. auch Niedersächsisches Kultusministerium (Hg.): Rahmenrichtlinien für das Gymnasium, S. 19. Zurück
26 siehe Bild der Lerngruppe. Zurück
27 ebd. Zurück
28 siehe Sachanalyse. Zurück
| Geschichte | Mathematik | Quilts | Home | Mailto |